# Verilog 学习笔记 - 练习题总结（Part 2）

# 有限状态机 (FSM)

用三组例题进行讲解

# 题组一：Lemmings 游戏

# 题目来源：hdlbits, exams/ece241_2013_q4

# Easy: Lemmings 1

The game Lemmings involves critters with fairly simple brains. So simple that we are going to model it using a finite state machine.

In the Lemmings' 2D world, Lemmings can be in one of two states: walking left or walking right. It will switch directions if it hits an obstacle. In particular, if a Lemming is bumped on the left, it will walk right. If it's bumped on the right, it will walk left. If it's bumped on both sides at the same time, it will still switch directions.

Implement a Moore state machine with two states, two inputs, and one output that models this behaviour.

	module top_module(
	input clk,
	input areset, // Freshly brainwashed Lemmings walk left.
	input bump_left,
	input bump_right,
	output walk_left,
	output walk_right); //

	parameter LEFT=0, RIGHT=1;
	reg state, next_state;

	always @(*) begin
	case(state)
	LEFT: next_state = (bump_left == 1) ? RIGHT : LEFT;
	RIGHT: next_state = (bump_right == 1) ? LEFT : RIGHT;
	endcase
	end

	always @(posedge clk, posedge areset) begin
	if(areset) state <= LEFT;
	else state <= next_state;
	end

	assign walk_left = (state == LEFT);
	assign walk_right = (state == RIGHT);

	endmodule

Easy 难度，按照题意模拟即可，只有两个状态 LEFT 和 RIGHT

# Hard: Lemmings 2

In addition to walking left and right, Lemmings will fall (and presumably go "aaah!") if the ground disappears underneath them.

In addition to walking left and right and changing direction when bumped, when ground=0 , the Lemming will fall and say "aaah!". When the ground reappears ( ground=1 ), the Lemming will resume walking in the same direction as before the fall. Being bumped while falling does not affect the walking direction, and being bumped in the same cycle as ground disappears (but not yet falling), or when the ground reappears while still falling, also does not affect the walking direction.

Build a finite state machine that models this behaviour.

	module top_module(
	input clk,
	input areset, // Freshly brainwashed Lemmings walk left.
	input bump_left,
	input bump_right,
	input ground,
	output walk_left,
	output walk_right,
	output aaah );

	parameter L = 0, R = 1, FL = 2, FR = 3;

	reg [1:0] state, next_state;

	always @(*) begin
	case(state)
	L: begin
	if(ground == 0) next_state = FL;
	else if(bump_left == 1) next_state = R;
	else next_state = L;
	end
	R: begin
	if(ground == 0) next_state = FR;
	else if(bump_right == 1) next_state = L;
	else next_state = R;
	end
	FL: begin
	if(ground == 1) begin
	/*if(bump_left == 1) next_state = R;
	else next_state = L;*/
	next_state = L;
	end
	else next_state = FL;
	end
	FR: begin
	if(ground == 1) begin
	/*if(bump_right == 1) next_state = L;
	else next_state = R;*/
	next_state = R;
	end
	else next_state = FR;
	end
	endcase
	end

	always @(posedge clk, posedge areset) begin
	if(areset) state <= L;
	else state <= next_state;
	end

	always @(*) begin
	if(state == FL \|\| state == FR) aaah = 1;
	else aaah = 0;
	walk_left = (state == L);
	walk_right = (state == R);
	end

	endmodule

Hard 难度，考虑到题目要求下落的情况，需要增加两种状态，因为下落不改变原来的方向，同时需要注意下落优先级高于转身，所以下落过程中 bump_left 和 bump_right 都没有效果

# Expert: Lemmings 3

In addition to walking and falling, Lemmings can sometimes be told to do useful things, like dig (it starts digging when dig=1 ). A Lemming can dig if it is currently walking on ground ( ground=1 and not falling), and will continue digging until it reaches the other side ( ground=0 ). At that point, since there is no ground, it will fall (aaah!), then continue walking in its original direction once it hits ground again. As with falling, being bumped while digging has no effect, and being told to dig when falling or when there is no ground is ignored.

(In other words, a walking Lemming can fall, dig, or switch directions. If more than one of these conditions are satisfied, fall has higher precedence than dig, which has higher precedence than switching directions.)

Extend your finite state machine to model this behaviour.

	module top_module(
	input clk,
	input areset, // Freshly brainwashed Lemmings walk left.
	input bump_left,
	input bump_right,
	input ground,
	input dig,
	output walk_left,
	output walk_right,
	output aaah,
	output digging
	);

	parameter L = 0, R = 1, FL = 2, FR = 3, DL = 4, DR = 5;

	reg [2:0] state, next_state;

	always @(*) begin
	case(state)
	L: begin
	if(ground == 0) next_state = FL;
	else if(dig == 1) next_state = DL;
	else if(bump_left == 1) next_state = R;
	else next_state = L;
	end
	R: begin
	if(ground == 0) next_state = FR;
	else if(dig == 1) next_state = DR;
	else if(bump_right == 1) next_state = L;
	else next_state = R;
	end
	FL:
	if(ground == 1) next_state = L;
	else next_state = FL;
	FR:
	if(ground == 1) next_state = R;
	else next_state = FL;
	DL: begin
	if(ground == 0) next_state = FL;
	else next_state = DL;
	end
	DR: begin
	if(ground == 0) next_state = FR;
	else next_state = DR;
	end
	default: next_state = state;
	endcase
	end

	always @(posedge clk, posedge areset) begin
	if(areset) state <= L;
	else state <= next_state;
	end

	always @(*) begin
	if(state == FL \|\| state == FR) aaah = 1;
	else aaah = 0;
	walk_left = (state == L);
	walk_right = (state == R);
	digging = state == DL \|\| state == DR;
	end

	endmodule

Expert 难度，考虑挖矿不会改变方向，但是可能会掉落，同时挖矿时 bump_left 和 bump_right 也都没有效果

# Special: Lemmings 4

Although Lemmings can walk, fall, and dig, Lemmings aren't invulnerable. If a Lemming falls for too long then hits the ground, it can splatter. In particular, if a Lemming falls for more than 20 clock cycles then hits the ground, it will splatter and cease walking, falling, or digging (all 4 outputs become 0), forever (Or until the FSM gets reset). There is no upper limit on how far a Lemming can fall before hitting the ground. Lemmings only splatter when hitting the ground; they do not splatter in mid-air.

Extend your finite state machine to model this behaviour.

Falling for 20 cycles is survivable, Falling for 21 cycles causes splatter.

本题的难度在于，考虑下落过程需要设置计数器，判断是否超过 20 个时钟周期，这时边界条件就非常麻烦，同时计数器必须单独写在一个 always 语句块中，否则会报错

对了，这一题比较坑的是计数器寄存器要足够大，否则会溢出！！！

	module top_module(
	input clk,
	input areset, // Freshly brainwashed Lemmings walk left.
	input bump_left,
	input bump_right,
	input ground,
	input dig,
	output walk_left,
	output walk_right,
	output aaah,
	output digging
	);

	parameter L = 0, R = 1, FL = 2, FR = 3, DL = 4, DR = 5, WASTED = 6;

	reg [2:0] state, next_state;

	reg [6:0] fall_time_cnt;

	always @(*) begin
	case(state)
	L: begin
	if(ground == 0) next_state = FL;
	else if(dig == 1) next_state = DL;
	else if(bump_left == 1) next_state = R;
	else next_state = L;
	end
	R: begin
	if(ground == 0) next_state = FR;
	else if(dig == 1) next_state = DR;
	else if(bump_right == 1) next_state = L;
	else next_state = R;
	end
	FL:
	if(ground == 1) begin
	if(fall_time_cnt > 20) next_state = WASTED;
	else next_state = L;
	end
	else next_state = FL;
	FR:
	if(ground == 1) begin
	if(fall_time_cnt > 20) next_state = WASTED;
	else next_state = R;
	end
	else next_state = FR;
	DL: begin
	if(ground == 0) next_state = FL;
	else next_state = DL;
	end
	DR: begin
	if(ground == 0) next_state = FR;
	else next_state = DR;
	end
	WASTED: next_state = WASTED;
	default: next_state = state;
	endcase
	end

	always @(posedge clk, posedge areset) begin
	if(areset) state <= L;
	else state <= next_state;
	end

	always @(posedge clk, posedge areset) begin
	if(areset) fall_time_cnt <= 0;
	else if(next_state == FL \|\| next_state == FR) fall_time_cnt <= fall_time_cnt + 1;
	else fall_time_cnt <= 0;
	end

	always @(*) begin
	if(state == WASTED) {aaah, walk_left, walk_right, digging} = 4'b0000;
	else begin
	if(state == FL \|\| state == FR) aaah = 1;
	else aaah = 0;
	walk_left = (state == L);
	walk_right = (state == R);
	digging = state == DL \|\| state == DR;
	end
	end

	endmodule

# 题组二：PS/2 鼠标协议

# Easy：信息校验

The PS/2 mouse protocol sends messages that are three bytes long. However, within a continuous byte stream, it's not obvious where messages start and end. The only indication is that the first byte of each three byte message always has bit[3]=1 (but bit[3] of the other two bytes may be 1 or 0 depending on data).

We want a finite state machine that will search for message boundaries when given an input byte stream. The algorithm we'll use is to discard bytes until we see one with bit[3]=1 . We then assume that this is byte 1 of a message, and signal the receipt of a message once all 3 bytes have been received ( done ).

The FSM should signal done in the cycle immediately after the third byte of each message was successfully received.

注意题目的意思是，一直找到 bit[3]=1 的作为开始，然后读取两个 byte，这时候把 done 设置为 1 表示接受完毕，然后再一直找到下一个 bit[3]=1 重新开始，这是一个简单的 Moore 型状态机

	module top_module(
	input clk,
	input [7:0] in,
	input reset, // Synchronous reset
	output done); //

	parameter S1 = 0, S2 = 1, S3 = 2, FINISH = 3;

	reg [1:0] state, next_state;

	// State transition logic (combinational)
	always @(*) begin
	case(state)
	S1: next_state = in[3] == 1 ? S2 : S1;
	S2: next_state = S3;
	S3: next_state = FINISH;
	FINISH: next_state = in[3] == 1 ? S2 : S1;
	endcase
	end

	// State flip-flops (sequential)
	always @(posedge clk) begin
	if(reset) state <= S1;
	else state <= next_state;
	end

	// Output logic
	assign done = state == FINISH;

	endmodule

# Expert：实现输出数据流

Now that you have a state machine that will identify three-byte messages in a PS/2 byte stream, add a datapath that will also output the 24-bit (3 byte) message whenever a packet is received ( out_bytes[23:16] is the first byte, out_bytes[15:8] is the second byte, etc.).

out_bytes needs to be valid whenever the done signal is asserted. You may output anything at other times (i.e., don't-care).

要输出数据流，我们需要单独使用一组寄存器及时记录数据，但是要注意 FINISH 不一定会转移回 S1，也有可能转移回 S2，因此记录数据要特殊考虑

	module top_module(
	input clk,
	input [7:0] in,
	input reset, // Synchronous reset
	output reg [23:0] out_bytes,
	output done); //

	// FSM from fsm_ps2

	parameter S1 = 0, S2 = 1, S3 = 2, FINISH = 3;

	reg [1:0] state, next_state;
	reg [23:0] temp;

	// State transition logic (combinational)
	always @(*) begin
	case(state)
	S1: next_state = in[3] == 1 ? S2 : S1;
	S2: next_state = S3;
	S3: next_state = FINISH;
	FINISH: next_state = in[3] == 1 ? S2 : S1;
	endcase
	end

	// State flip-flops (sequential)
	always @(posedge clk) begin
	if(reset) state <= S1;
	else begin
	state <= next_state;
	out_bytes <= (state == FINISH) ? 0 : temp; // 其实也没必要这样，因为题意是 done 不是 1 时输出什么都无所谓
	end
	end

	always @(*) begin
	case(state)
	S3: temp[7:0] = in[7:0];
	S2: temp[15:8] = in[7:0];
	S1: temp[23:16] = in[7:0];
	default: temp = 0;
	endcase
	if(state == FINISH && next_state == S2) temp[23:16] = in[7:0]; // 这里就是特殊判断上述分析中的情况
	end


	// Output logic
	assign done = state == FINISH;
	// New: Datapath to store incoming bytes.

	endmodule

# 题组三：通信协议

# Normal：数据校验

In many (older) serial communications protocols, each data byte is sent along with a start bit and a stop bit, to help the receiver delimit bytes from the stream of bits. One common scheme is to use one start bit (0), 8 data bits, and 1 stop bit (1). The line is also at logic 1 when nothing is being transmitted (idle).

Design a finite state machine that will identify when bytes have been correctly received when given a stream of bits. It needs to identify the start bit, wait for all 8 data bits, then verify that the stop bit was correct. If the stop bit does not appear when expected, the FSM must wait until it finds a stop bit before attempting to receive the next byte.

跟上面一组题类似，注意考虑何时将 done 置为 1，另外本题就使用了 Lemmings 4 中的计数器方法，因为要重复读取 8 个字符

	module top_module(
	input clk,
	input in,
	input reset, // Synchronous reset
	output done
	);
	parameter START = 0, WAIT = 1, DONE = 2, ERROR = 3;
	reg [1:0] state, next_state;
	reg [31:0] wait_time_cnt;

	always @(*) begin
	case(state)
	START: next_state = (in == 0) ? WAIT : START;
	WAIT: begin
	if(wait_time_cnt > 8) next_state = (in == 1) ? DONE : ERROR;
	else next_state = WAIT;
	end
	DONE: next_state = (in == 0) ? WAIT : START;
	ERROR: next_state = (in == 1) ? START : ERROR;
	endcase
	end

	always @(posedge clk) begin
	if(reset) state <= START;
	else state <= next_state;
	end

	always @(posedge clk) begin
	if(reset) wait_time_cnt <= 0;
	else if(next_state == WAIT) wait_time_cnt <= wait_time_cnt + 1;
	else wait_time_cnt <= 0;
	end

	assign done = (state == DONE);

	endmodule

# Expert：输出数据流

Now that you have a finite state machine that can identify when bytes are correctly received in a serial bitstream, add a datapath that will output the correctly-received data byte. out_byte needs to be valid when done is 1 , and is don't-care otherwise.

Note that the serial protocol sends the least significant bit first.

这里注意何时输出，在我的代码里需要当 next_state == DONE 时输出，这样可以防止把最后一个符号位 1 也读进去

	module top_module(
	input clk,
	input in,
	input reset, // Synchronous reset
	output [7:0] out_byte,
	output done
	); //

	// Use FSM from Fsm_serial
	parameter START = 0, WAIT = 1, DONE = 2, ERROR = 3;
	reg [1:0] state, next_state;
	reg [31:0] wait_time_cnt;
	reg [7:0] temp_list;

	always @(*) begin
	case(state)
	START: next_state = (in == 0) ? WAIT : START;
	WAIT: begin
	if(wait_time_cnt > 7) next_state = (in == 1) ? DONE : ERROR; // 读入第 8 个数据时就要考虑下一个状态是啥了
	else next_state = WAIT;
	end
	DONE: next_state = (in == 0) ? WAIT : START;
	ERROR: next_state = (in == 1) ? START : ERROR;
	endcase
	end

	always @(posedge clk) begin
	if(reset) state <= START;
	else state <= next_state;
	if(next_state == DONE) out_byte <= temp_list;
	else out_byte <= 0;
	end

	always @(posedge clk) begin
	if(reset) wait_time_cnt <= 0;
	else if(state == WAIT) wait_time_cnt <= wait_time_cnt + 1;
	else wait_time_cnt <= 0;
	end

	always @(posedge clk) begin
	if(state == WAIT) begin
	temp_list[7:0] = {in, temp_list[7:1]};
	end
	end

	assign done = (state == DONE);
	// New: Datapath to latch input bits.

	endmodule

# Lunatic：奇偶校验

We want to add parity checking to the serial receiver. Parity checking adds one extra bit after each data byte. We will use odd parity, where the number of 1 s in the 9 bits received must be odd. For example, 101001011 satisfies odd parity (there are 5 1 s), but 001001011 does not.

Change your FSM and datapath to perform odd parity checking. Assert the done signal only if a byte is correctly received and its parity check passes. Like the serial receiver FSM, this FSM needs to identify the start bit, wait for all 9 (data and parity) bits, then verify that the stop bit was correct. If the stop bit does not appear when expected, the FSM must wait until it finds a stop bit before attempting to receive the next byte.

You are provided with the following module that can be used to calculate the parity of the input stream (It's a TFF with reset). The intended use is that it should be given the input bit stream, and reset at appropriate times so it counts the number of 1 bits in each byte.

module parity (
    input clk,
    input reset,
    input in,
    output reg odd);

    always @(posedge clk)
        if (reset) odd <= 0;
        else if (in) odd <= ~odd;

endmodule

Note that the serial protocol sends the least significant bit first, and the parity bit after the 8 data bits.

~~刚开始貌似脑袋坏掉了，做了半天，重构一遍代码之后想起来好像扩充状态数后 reg 的长度没增加...... 最近睡得有点少......~~

但是实际上这一题不需要增加状态数，可以把奇偶校验位放在 WAIT 状态中处理

	module top_module(
	input clk,
	input in,
	input reset, // Synchronous reset
	output [7:0] out_byte,
	output done
	); //

	// Use FSM from Fsm_serial
	parameter START = 0, WAIT = 1, DONE = 2, ERROR = 3;
	reg [1:0] state, next_state;
	reg [31:0] wait_time_cnt;
	reg [7:0] temp_list;
	reg parity_checker, parity_ans;

	parity parity_check(.clk(clk), .in(in), .reset(!(state == WAIT)), .odd(parity_checker));

	always @(*) begin
	case(state)
	START: next_state = (in == 0) ? WAIT : START;
	WAIT: begin
	if(wait_time_cnt > 8) next_state = (in == 1) ? DONE : ERROR;
	else next_state = WAIT;
	end
	DONE: next_state = (in == 0) ? WAIT : START;
	ERROR: next_state = (in == 1) ? START : ERROR;
	endcase
	end

	always @(posedge clk) begin
	if(reset) state <= START;
	else state <= next_state;
	if(next_state == DONE) out_byte <= temp_list;
	else out_byte <= 0;
	end

	always @(posedge clk) begin
	if(reset) wait_time_cnt <= 0;
	else if(state == WAIT) wait_time_cnt <= wait_time_cnt + 1;
	else wait_time_cnt <= 0;
	if(wait_time_cnt == 9) parity_ans <= parity_checker;
	end

	always @(posedge clk) begin
	if(state == WAIT && wait_time_cnt != 8) begin
	temp_list[7:0] = {in, temp_list[7:1]};
	end
	end

	assign done = (state == DONE) & parity_ans;
	// New: Datapath to latch input bits.

	endmodule

# 关于序列识别

注意到课上测试和课下测试中关于 FSM 的题目大部分都是正则表达式匹配和自动售货机问题，这里单独把序列识别拎出来分析一下

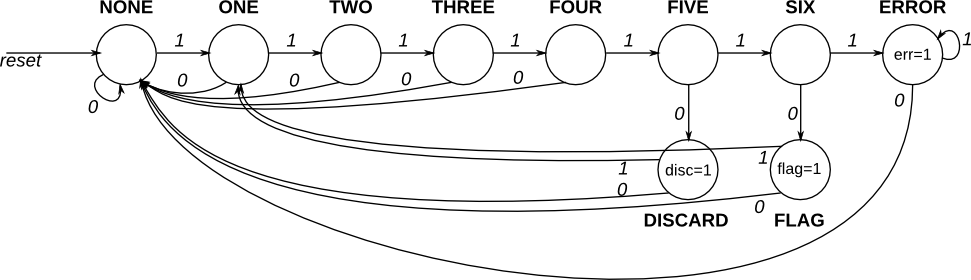
Synchronous HDLC framing involves decoding a continuous bit stream of data to look for bit patterns that indicate the beginning and end of frames (packets). Seeing exactly 6 consecutive 1s (i.e., 01111110 ) is a "flag" that indicate frame boundaries. To avoid the data stream from accidentally containing "flags", the sender inserts a zero after every 5 consecutive 1s which the receiver must detect and discard. We also need to signal an error if there are 7 or more consecutive 1s.

Create a finite state machine to recognize these three sequences:

0111110 : Signal a bit needs to be discarded ( disc ).
01111110 : Flag the beginning/end of a frame ( flag ).
01111111... : Error (7 or more 1s) ( err ).

When the FSM is reset, it should be in a state that behaves as though the previous input were 0.

Implement this state machine.

目标是识别所有的 01111110 结尾的序列，并标记为 disc ，这种序列用正则表达式可以写为 ^01{6}0

	module top_module(
	input clk,
	input reset, // Synchronous reset
	input in,
	output disc,
	output flag,
	output err);

	parameter START = 0, WAIT = 1;
	reg state, next_state;
	reg [31:0] wait_time_cnt;

	always @(*) begin
	case(state)
	START: next_state = (in == 1) ? WAIT : START;
	WAIT: begin
	if(in == 1) next_state = WAIT;
	else next_state = START;
	end
	endcase
	end

	always @(posedge clk) begin
	if(reset) state <= START;
	else state <= next_state;
	end

	always @(posedge clk) begin
	if(reset) {disc, flag, err} <= 3'b000;
	else begin
	case(state)
	START:{disc, flag, err} <= 3'b000;
	WAIT: begin
	if(wait_time_cnt == 5 && next_state == START) {disc, flag, err} <= 3'b100;
	else if(wait_time_cnt == 6 && next_state == START) {disc, flag, err} <= 3'b010;
	else if(wait_time_cnt > 5 && next_state == WAIT) {disc, flag, err} <= 3'b001;
	else {disc, flag, err} <= 3'b000;
	end
	endcase
	end
	end

	always @(posedge clk) begin
	if(reset) wait_time_cnt <= 0;
	else if(next_state == WAIT) wait_time_cnt <= wait_time_cnt + 1;
	else wait_time_cnt <= 0;
	end

	endmodule

受不了这个计数器方法了，我调了一个小时可还行...... 下次我直接这样做......

Fsm hdlc.png