# 时序电路斐波那契电路分析与题解

# 题目描述

使用 Logisim 搭建电路，使得只需要 64 个周期就能计算出 32 位无符号整数能表示的最大数位置上的斐波那契数的最后 32bit

输入序号 $x$ ，输出对应序号斐波那契数 $F_x$

具体要求：

$F_0=0,F_1=1,F_{n}=F_{n-1}+F_{n-2}(n\geqslant2)$
输入： $N$ （32bit 无符号数）
输出： $N_{th}$ （32bit 无符号数，表示第 $N$ 个斐波那契数）
文件内模块名: main
HINT：矩阵乘法的快速幂

# 分析

HINT：矩阵乘法的快速幂

# 什么是矩阵乘法的快速幂？

一句话：矩阵快速幂 = 矩阵乘法 + 快速幂

矩阵乘法大家应该很熟悉了，问题应该是：

# 什么是快速幂呢？

快速幂基于以下原理：对于任意一个数，都可以拆成 $2^k$ 的数构成的和，所以求 $a^b$ 可以把它拆成某几个 $a^{2^k}$ 的积

例如： $3^{11}=3^{8+2+1}=3^8\times3^2\times3^1$

那么我们应该容易看出来，如果将 11 用二进制表示为 $(1011)_2$ ，则从左往右数第 $n$ 位为 1，则结果乘上 $3^{2^n}$ 即可

由于矩阵乘法也满足结合律，因此我们可以用相似的方法求出矩阵的任意次幂

关于矩阵快速幂，有模板题 P3390 【模板】矩阵快速幂 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

# 本题与矩阵有什么关系？

~~众所周知~~，斐波那契数列还可以这样求，记 $F_n$ 为斐波那契额数列的第 $n$ 项，则有：

$\begin{bmatrix} F_{n+1}\\ F_n \end{bmatrix} = \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^n \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix}$

因此求第 $n$ 项的问题转化为求矩阵乘法的问题，自然可以用快速幂解决

# 划分子问题

# 矩阵乘法

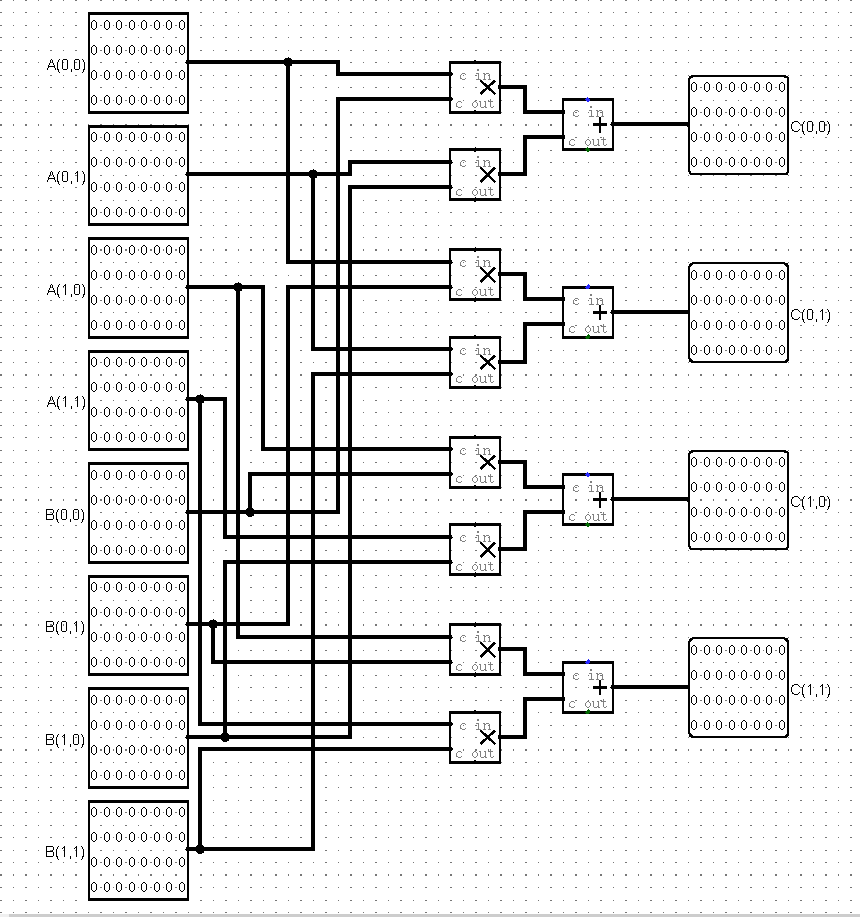
首先很容易想到需要实现的，也很容易画出电路图的应该是矩阵乘法模块

模块名：matrix_mul

# 处理输入数据

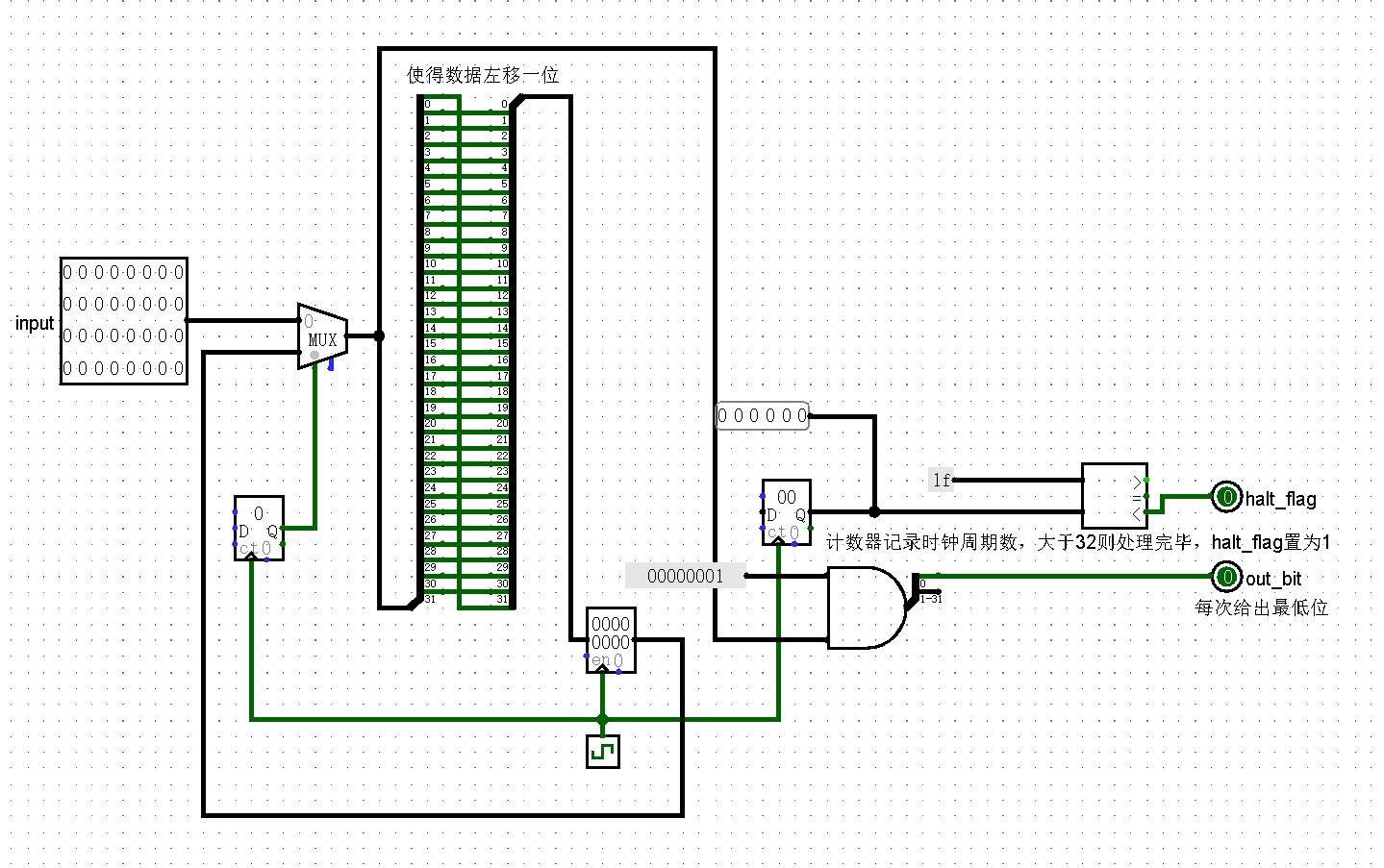
按位处理，每一个时钟周期上升沿让数据左移一位，每一次将数字 and 上 1 则可以取到最低位，使用计数器记录时钟周期，当计数器大于 32 时则每一位都处理完毕，则可以输出结果，模块名：get_bit

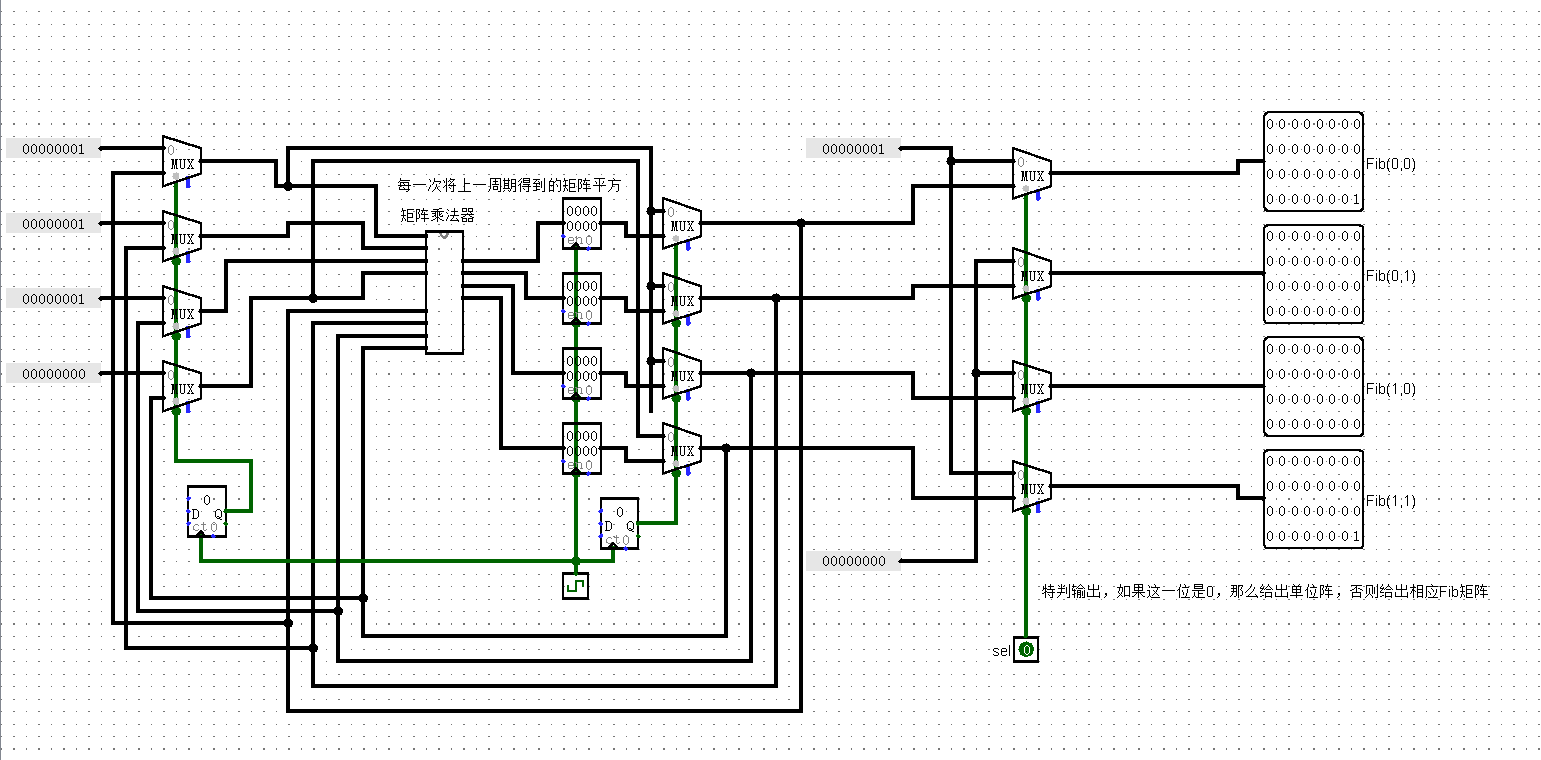
# 生成所需要的 Fib 矩阵

我们记 Fib 矩阵为

$Fib = \begin{bmatrix}1 & 1\\ 1 & 0\end{bmatrix}$

在每一个时钟周期，我们都将 Fib 矩阵平方，这样我们在处理第 $n$ 位时可以得到

$\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^{2^n}$

但是有可能第 $n$ 位为 0，这时不需要乘上 Fib 矩阵的 $2^n$ 次幂，此时我们用多路选择器判断，并给出单位矩阵 $E$ 去做乘法

模块名：get_fib_matrix

# main 模块

main 模块是主体流程和模块整合

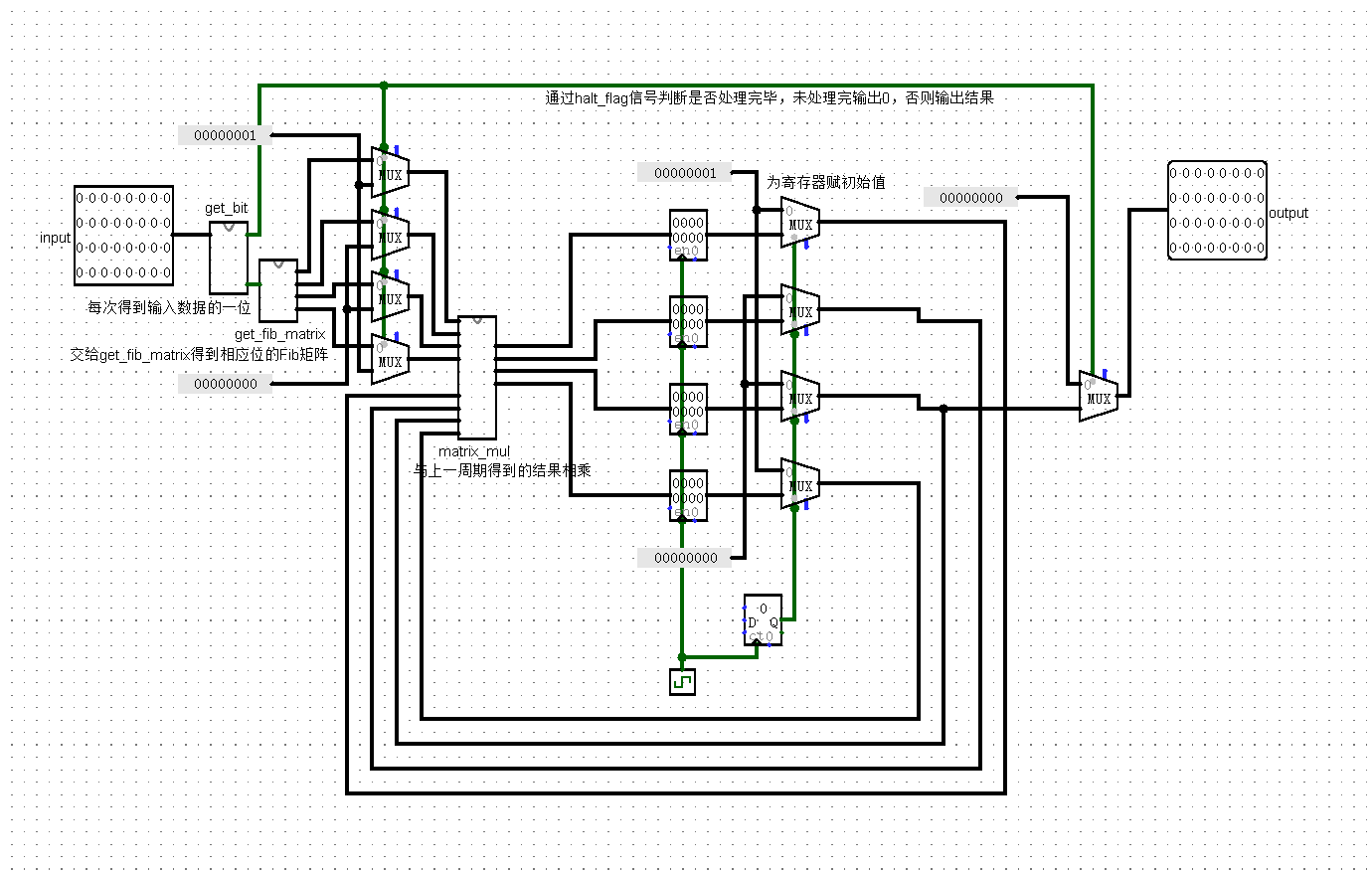
有一点，所谓为寄存器赋初始值，并不是真正 “写” 一个值进入寄存器内部，而是判断还没到第一个时钟周期上升沿时，利用多路选择器输出一个自定义的值

# 总结与反思

一定要注意初始值处理，在为矩阵赋初始值时，哪里赋值为单位矩阵，哪里赋值为 Fib 矩阵
只判断到第 32 个周期是不够的，这样不能处理最高位 (~~我第一次提交就卡在了这里~~)，必须当计数器的值大于 0x1f 时才能判断处理结束

# 时序电路 斐波那契电路 分析与题解